Model Checking of Infinite-State Systems using Narrowing


Introduction

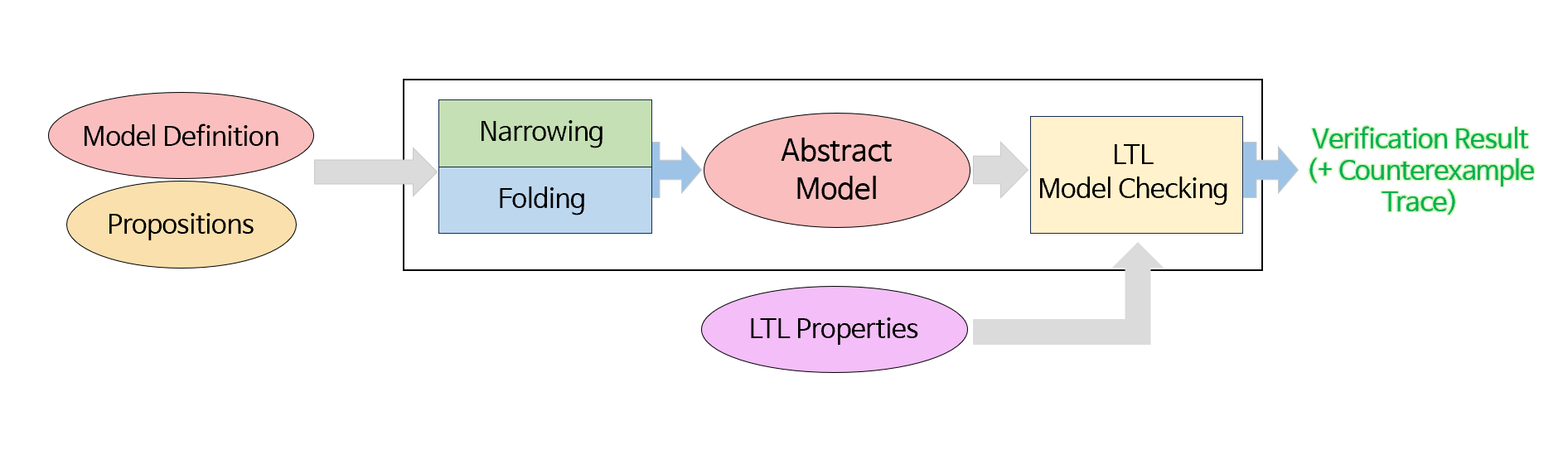
Figure 1: High-level architecture of the pattern-based Logical Model Checker (LMC).

Formal verification aims to mathematically prove the correctness of a system against a given specification. Model checking is a powerful automated technique for this, but it traditionally struggles with infinite-state systems—systems where the number of possible states is unbounded, such as systems with counters, timers, or dynamic process creation. In these cases, exhaustively exploring every state is impossible.

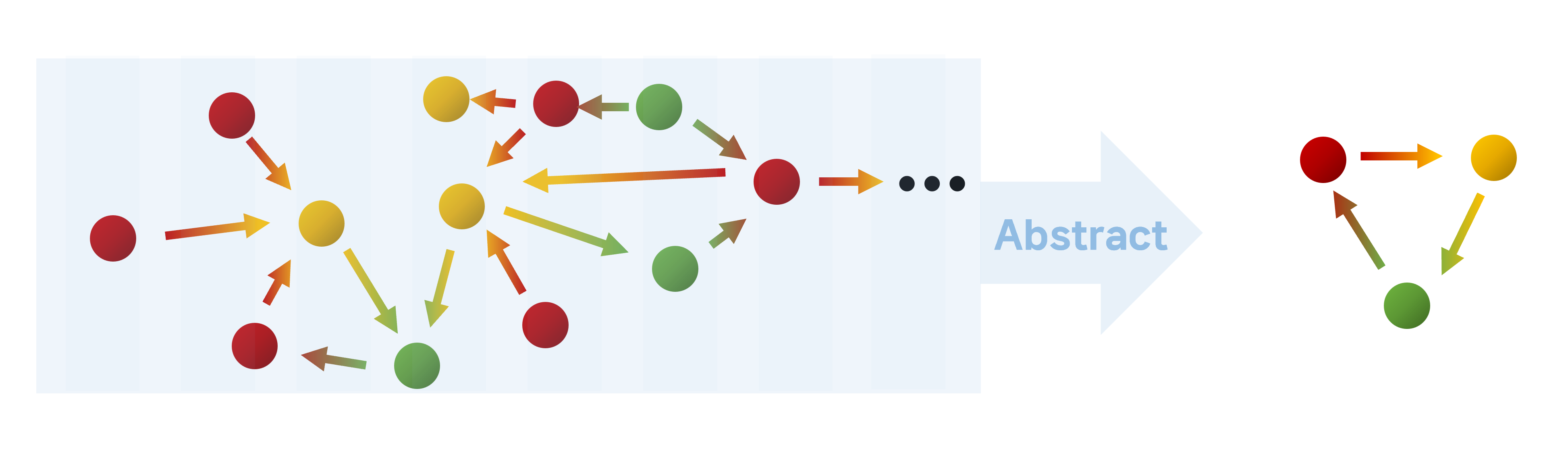
Figure 2: The core idea of infinite-state model checking is to symbolically summarize an infinite number of concrete states into a finite number of abstract patterns.

To address this challenge, our research focuses on pattern-based symbolic model checking. This approach represents infinite sets of concrete states using a finite number of symbolic patterns. Our work extends the Logical Model Checker (LMC), a tool based on a symbolic model checking algorithm that uses Narrowing and Folding to analyze system behavior. LMC can verify critical temporal properties expressed in Linear Temporal Logic (LTL).

However, the applicability of the original LMC is limited. It requires systems to satisfy the Finite Variant Property in its narrowing process. Our goal is to expand the scope and power of LMC, transforming it into a practical tool for verifying complex software, such as security and concurrency protocols, and contributing to the prevention of subtle bugs.

Framework: Extending the Logical Model Checker

Our approach enhances LMC with new capabilities to analyze a much wider spectrum of infinite-state systems. The framework is built on two major extensions: a more expressive state representation and a sound method for state space reduction.

Extended State Representation with Constraints

The first limitation we address is the inability of standard narrowing to handle all types of equational theories or system properties. For example, verifying Lamport’s Bakery Algorithm is challenging because its correctness depends on properties that are difficult for narrowing to track.

To overcome this, we enrich the state representation. Instead of a simple pattern, a state is now a pair: State = (Pattern, Constraints)

To support this, we introduce incomplete propositions. These are logical conditions where we explicitly define when they evaluate to true but leave other cases undefined (incomplete). When the model checker encounters an incomplete proposition during analysis, it doesn’t fail; instead, it propagates the condition as a constraint attached to the new symbolic state. This allows the verification of systems with non-deterministic transitions and complex conditional logic that were previously out of reach.

User-Definable State Space Reduction

Even with symbolic methods, the abstract state space can still be too large or complex. Our second major contribution is a framework for further simplifying the state space using user-defined reduction rules (simplification rules).

The core challenge is ensuring that these user-provided rules are sound—that is, the simplified system must be behaviorally equivalent to the original. The theoretical foundation for this soundness guarantee is Bisimulation.

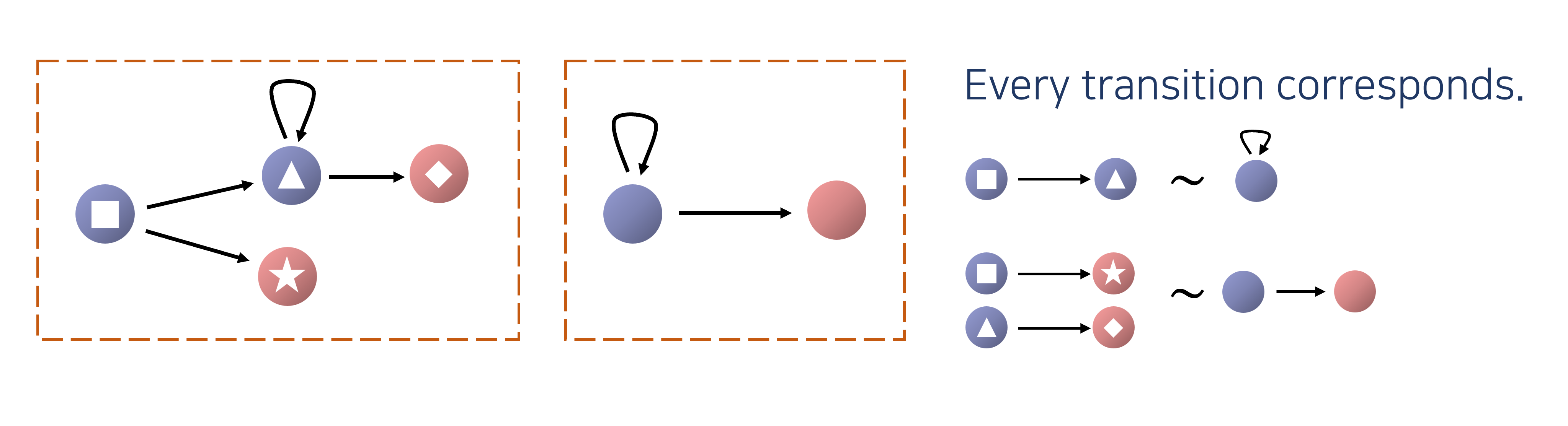
Figure 3: The Principle of Bisimulation. A reduction is sound if for every transition in the original system (from p to p'), there is a corresponding transition in the reduced system (from q to q') such that the resulting states (p' and q') are still related.

A reduction rule is considered sound if the reduced system maintains a bisimulation relation with the original system. This guarantees that any property verified on the smaller, simpler system also holds true for the original, complex one. This allows a user to leverage domain-specific knowledge to simplify the verification problem without compromising correctness.

Soundness Verification for User-Defined Reduction Rules

A critical component of our framework is the ability to automatically verify that a reduction rule supplied by a user is indeed sound. Manually proving bisimulation is tedious and error-prone. Therefore, we developed an algorithm to automate this soundness check.

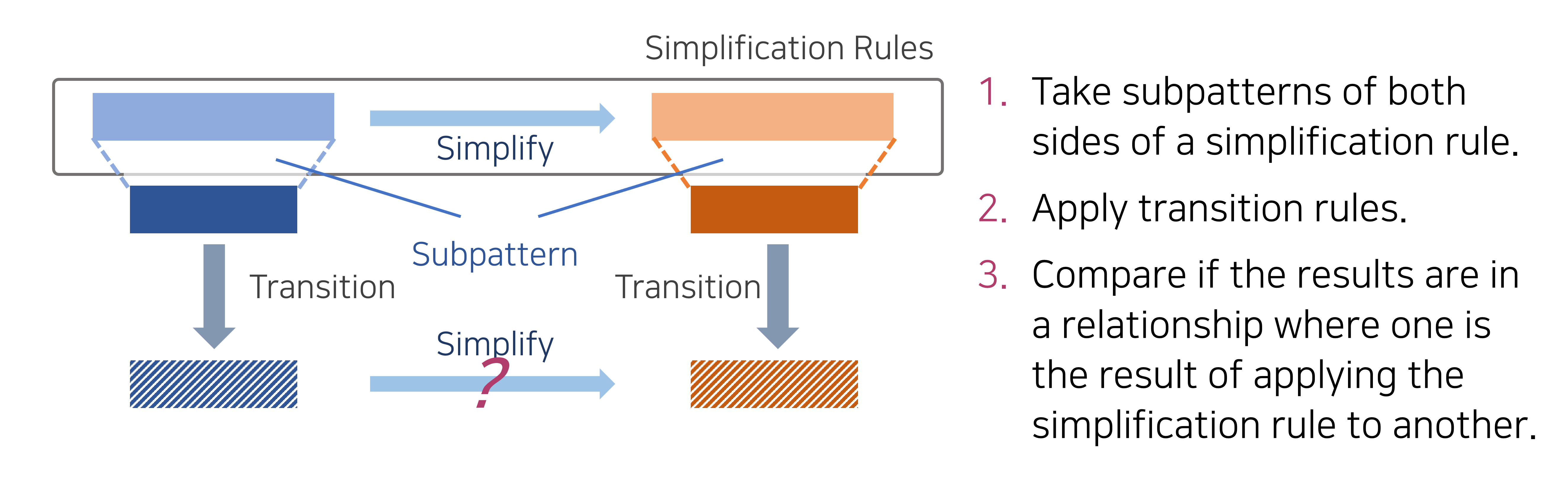
Figure 4: The automated workflow for verifying and applying user-defined reduction rules.

Our proposed algorithm works as follows:

  1. Input: A user-defined reduction rule, which equates a complex pattern with a simpler one.
  2. Process: The algorithm systematically explores the behavior of both patterns. It applies all possible system transitions (via narrowing) to the complex pattern.
  3. Verification: For each resulting state, it checks if it can be matched by a corresponding transition from the simpler pattern, such that the new pair of states still satisfies the reduction rule.
  4. Output: The algorithm confirms whether the rule preserves bisimulation across all possible transitions. If it does, the rule is deemed sound and can be safely used by the model checker to reduce the state space.

This automated check is essential for making the state-space reduction technique practical and reliable.

Future Work

Automatic Generation of Valid Reduction Rules

While verifying user-defined rules is a major step forward, the ultimate goal is to make infinite-state model checking more accessible by reducing the need for expert intervention. Finding effective and sound reduction rules remains a difficult task that requires deep insight into both the system and the verification theory.

Our future work will focus on techniques to automatically generate valid reduction rules. We are investigating two primary approaches:

  1. Static Analysis: Develop algorithms that analyze the system’s transition rules before model checking begins. By identifying recurring structural patterns and symmetries, these algorithms could propose valid simplification rules automatically.
  2. Dynamic Generation: Integrate rule generation into the model checking process itself. When the checker encounters a new, complex state pattern, it would trigger a routine that attempts to find a simpler, bisimilar representation for it on-the-fly.

By combining automatic generation with our existing soundness checker, we aim to create a powerful, highly automated verification framework capable of tackling an even broader range of challenging problems.

Case Studies & Benchmarks

To validate our approach, we are applying our extended LMC to a set of well-known and challenging concurrency algorithms. These serve as benchmarks to demonstrate the increased expressiveness and power of our framework. Case studies include:

Successfully verifying these systems demonstrates the practical utility of our constraint-based and reduction-based extensions.

References

Contact

Kyunwoo Kim kkw423 (at) postech.ac.kr