SMT-Based Model Checking for Signal Temporal Logic

Abstract

Signal temporal logic (STL) is widely used to specify and analyze properties of cyber-physical systems (CPS) with continuous behaviors. We present an algorithm that can guarantee the correctness of CPS up to bounds. We reduce the bounded model checking problem of an STL formula for a hybrid automaton to the satisfiability of a first-order encoding using the algorithm and solve the satisfiability problem using a SMT solver. We implement the algorithm. The tool supports Z3 and Yices2 as the underlying SMT solver. We have compared the performance of our algorithm [1] and the previous algorithm [2]. Our algorithm outperforms other methods in most cases.

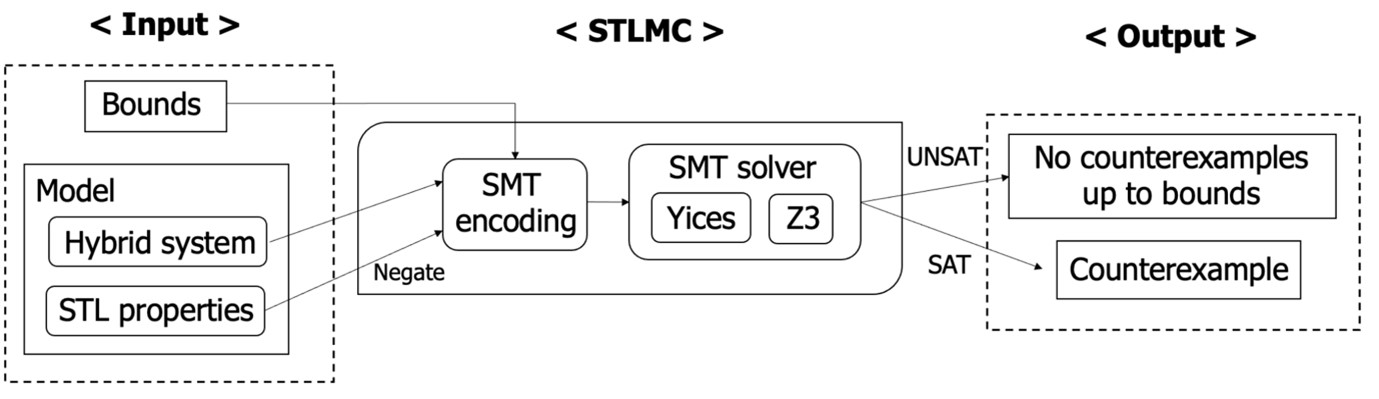
Overall architecture

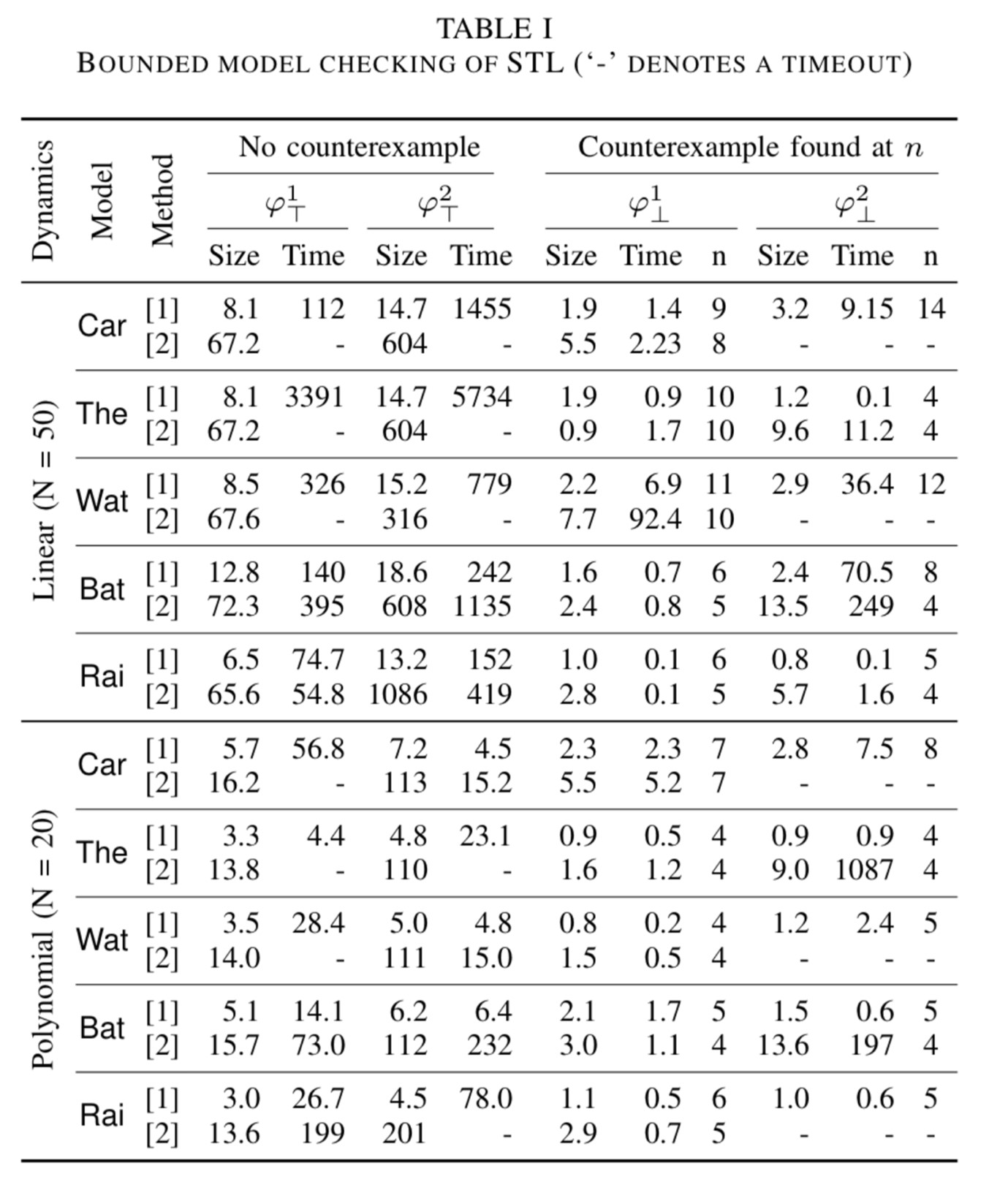
Experimental results

We consider the following hybrid automata models: autonomous cars (Car), thermostat (The), water tank (Wat) systems, load management of batteries (Bat), and railroad gate controllers (Bat), and railroad gate controllers (Rai). We use two variants of continuous dynamics: linear and polynomial of degree 2. For each model, we use four STL formulas: \(\varphi^d_{\top}\) holds, and \(\varphi^d_{\bot}\) has a counterexample, where \(d\) represents the nesting depth of the formula. More details on the benchmark models can be found in [1].

Reference

1. Jia Lee, Geunyeol Yu, and Kyungmin Bae. Efficient SMT-Based model checking for signal temporal logic. [paper, github]
2. Kyungmin Bae and Jia Lee. Bounded model checking of signal temporal logic properties using syntactic separation. Proceedings of the ACM on Programming Languages, vol. 3, no. POPL, pp. 1–30, 2019. [paper, github]